10 клас геометрія

 👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉

Паралельність площин

* * *

Додаткові матеріала для підготовки до контрольної роботи з геометрії

Он-лайн подорожі за сторінками підручника математики

Паралельність прямих у просторі

Доброго дня. Сьогодні ми з вами зустрічалися у Zoom конференції. Пропоную матеріали які були використані на цій зустрічі.

Також для звротнього зв'язку, прошу пройти невеликий тест. Не переживайте оцінювати ваші знання я в ньому сьогодні не буду.

Але прошу приєднатися для цього перейдіть за посиланням https://classroom.google.com/ 

Натисніть ПРИЄДНАТИСЯ (в правому верхньому кутку "+")

Введіть код 4f33nds

Урок № 13

Підсумковий контрольний тест 

   Вам пропонується виконати підсумковий контрольний тест, при цьому розв'язання цього тесту має бути на окремих подвійних аркушах у клітинку. Необхідно підписати аркуш відповідно до зразка та виконати усі завдання. Відповіді до тесту зараховуються автоматично, а фото аркуша з розв'язками ви надсилаєте на мою електронну адресу klasszavdanny@gmail.com. Оцінка буде зарахованою при наявності фото копії розв'язання тесту.

    

Пройдіть тестування за посиланням. Результат тесту зараховується лише з першої спроби. Не намагайтеся проходити тестування під іншими іменами та прізвищами. Ці дані фіксуються автоматично. Не забувайте підписати власне прізвище та ім'я!

Перейдіть за посиланням:   join.naurok.ua

використайте код доступу: 676024

Бажаю успіху!!!

Урок  № 12

Вектори

Поняття вектора Wikipedia

Означення: Вектор – це напрямлений відрізок.

Вектор має початок та кінець.

Графічно вектори зображаються у вигляді напрямлених відрізків певної довжини.

Напрям вектора задається стрілкою на його кінці.
Позначається вектор або малою латинською буквою зверху зі стрілкою , або двома великими буквами зі стрілкою , перша з яких є початком, а друга кінцем вектора.

Означення. Зв'язаним називається вектор, який має чітко визначений початок.

Означення. Вільним називається вектор, початок якого може бути перенесеним у будь-яку точку. Надалі розглядатимемо саме вільні вектори.

Означення: Абсолютною величиною або модулем вектора називається довжина відрізка, що зображує вектор. Позначається ||.

Означення: Два вектори називаються рівними, якщо їх модулі та напрямки є однаковими.
Нехай вектор  має початком точку , а кінцем - точку .
Означення: Координатами вектора  називаються числа .
Тобто, щоб визначити координати вектора, потрібно від координат кінця вектора відняти координати його початку.

Два вектори є рівними, якщо в них рівні відповідні координати.
Означення: Вектор, у якого початок збігається із його кінцем, називається нуль-вектором .
Модуль (довжина) вектора визначається за формулою: 

Вектори в просторі

Попередні формули, записані для двох координат, можуть бути поширені на три та більше координат.

Означення. Два вектори називаються колінеарними, якщо вони паралельні одній прямій.

Означення. Три вектори називаються компланарними, якщо вони паралельні одній площині.

Операції над векторами

Над вектором можна виконати такі операції:

1. Додавання (віднімання) двох векторів

Означення. Сумою двох векторів  та  називається вектор ().
Геометрично вектори можна додавати за правилами трикутника або паралелограма.
Означення. Різницею двох векторів  та  називається вектор =().

2. Множення вектора на число
Означення. Добутком вектора  на число  називається вектор
().
Геометрично це означає збільшення вектора  у  разів.
3. Множення векторів.

Скалярний добуток двох векторів

Означення. Скалярним добутком двох векторів  та  називається число .
Скалярний добуток двох векторів можна обчислити за іншою формулою: , де:  - кут між цими векторами.
З цієї формули можна отримати формулу для обчислення косинуса кута між векторами: .
Коли вектори перпендикулярні, то їх скалярний добуток дорівнює нулю, і навпаки.
Фізичним змістом скалярного добутку двох векторів є робота сили по переміщенню тіла: .

Операції над векторами у просторі

Попередні формули, записані для двох координат, можуть бути поширені на три та більше координат.
Крім вище описаних операцій, для векторів у просторі можна визначити векторний та змішаний добуток.

Векторний добуток двох векторів

Означення. Векторним добутком двох векторів  та  називається вектор =[] для якого:
1. , де:  - кут між векторами;
2.  ;
3. Вектори , взяті у такому порядку, утворюють праву трійку векторів.

Означення. Упорядкована трійка некомпланарних векторів називається правою, якщо з кінця третього вектора найкоротший поворот від першого вектора до другого здійснюється проти обертання годинникової стрілки.

1. Опишіть будову прямокутної системи координат у просторі. Яку назву мають координатні осі? Чому дорівнюють абсциса і апліката точки, що лежить на осі ординат? Чи правильно, що точка M(3;-2;0) лежить у площині xy?

2. За якою формулою знаходять відстань між двома точками у просторі, якщо відомі їхні координати? Чому дорівнює відстань між точками A(-1;2;0) і B(-2;-2;3)?

3. Як знайти координати середини відрізка, якщо відомі координати його кінців? Чи правильно, що середина відрізка AB належить площині yz, якщо A(-3;4;2), В(3;0;0)?

Бажаю успіху!!!



Урок № 11

Прямі та площини у просторі

Ми з вами продовжуємо повторювати вивчений матеріал.

Паралельність прямих у просторі

Якщо a||b, b||c, тоді a||c
Рис. 10. Три паралельні прямі

Якщо Ba, тоді
!b, Bb, b||a
Рис. 9.

Рис. 8. Мимобіжні прямі

Рис. 7. Паралельні прямі

Означення. Дві прямі в просторі називаються паралельними, якщо вони лежать в одній площині й не перетинаються (Рис. 7).

Означення. Прямі, які не перетинаються і не лежать в одній площині, називаються мимобіжними (Рис. 8).

Теорема. Через точку поза даною прямою можна провести пряму, паралельну цій прямій, і до того ж тільки одну (Рис. 9).

Теорема. Дві прямі, паралельні третій прямій, паралельні між собою (Рис. 10).

Паралельність прямої і площини у просторі

Якщо Bα, тоді !β, Bβ, β||α
Рис. 15. Паралельна площина
проведена через точку
поза даною площиною

Якщо aα, bα, a∩b=A,
β||a, β||b, тоді β||α
Рис. 14. Площина паралельна
до двох прямих другої площини

Рис. 13. Паралельні площини

Якщо bα, b||a, aα ,
тоді b||α
Рис. 12. Пряма, паралельна
до прямої на площині

Рис. 11. Пряма, паралельна
до площини

Якщо α||β, a||b, a∩α=A1,
a∩β=A2, b∩α=B1, b∩β=B2,
тоді A1A2 = B1B2
Рис. 17. Паралельні площини
перетинають паралельні прямі

Якщо α||β, γα, γβ,
γ∩α=a, γ∩β=b, тоді a||b
Рис. 16. Площина, яка
перетинає паралельні площини

Означення. Пряма і площина називаються паралельними, якщо вони не перетинаються (Рис. 11).

Теорема. Якщо пряма, яка не належить площині, паралельна якій-небудь прямій у цій площині, то вона паралельна і самій площині (Рис. 12).

Означення. Дві площини називаються паралельними, якщо вони не перетинаються (Рис. 13).

Теорема. Дві площини паралельні, якщо одна з них паралельна двом прямим, які лежать у другій площині і перетинаються (Рис. 14).

Теорема. Через точку поза даною площиною можна провести площину, паралельну даній, і до того ж тільки одну (Рис. 15).

Теорема. Якщо дві паралельні площини перетинаються третьою, то прямі їх перетину паралельні (Рис. 16).

Теорема. Відрізки паралельних прямих, які містяться між паралельними площинами, рівні (Рис. 17).

Для зворотнього зв'язку прошу пройти невеликий тест:
Перейдіть за посиланням  join.naurok.ua
Код доступу: 439107
Бажаю успіху!!!



Урок № 10

Прямі та площини у просторі

Ми з вами продовжуємо повторювати вивчений матеріал.

Паралельність прямих у просторі

Якщо a||b, b||c, тоді a||c
Рис. 10. Три паралельні прямі

Якщо Ba, тоді
!b, Bb, b||a
Рис. 9.

Рис. 8. Мимобіжні прямі

Рис. 7. Паралельні прямі

Означення. Дві прямі в просторі називаються паралельними, якщо вони лежать в одній площині й не перетинаються (Рис. 7).

Означення. Прямі, які не перетинаються і не лежать в одній площині, називаються мимобіжними (Рис. 8).

Теорема. Через точку поза даною прямою можна провести пряму, паралельну цій прямій, і до того ж тільки одну (Рис. 9).

Теорема. Дві прямі, паралельні третій прямій, паралельні між собою (Рис. 10).

Паралельність прямої і площини у просторі

Якщо Bα, тоді !β, Bβ, β||α
Рис. 15. Паралельна площина
проведена через точку
поза даною площиною

Якщо aα, bα, a∩b=A,
β||a, β||b, тоді β||α
Рис. 14. Площина паралельна
до двох прямих другої площини

Рис. 13. Паралельні площини

Якщо bα, b||a, aα ,
тоді b||α
Рис. 12. Пряма, паралельна
до прямої на площині

Рис. 11. Пряма, паралельна
до площини

Якщо α||β, a||b, a∩α=A1,
a∩β=A2, b∩α=B1, b∩β=B2,
тоді A1A2 = B1B2
Рис. 17. Паралельні площини
перетинають паралельні прямі

Якщо α||β, γα, γβ,
γ∩α=a, γ∩β=b, тоді a||b
Рис. 16. Площина, яка
перетинає паралельні площини

Означення. Пряма і площина називаються паралельними, якщо вони не перетинаються (Рис. 11).

Теорема. Якщо пряма, яка не належить площині, паралельна якій-небудь прямій у цій площині, то вона паралельна і самій площині (Рис. 12).

Означення. Дві площини називаються паралельними, якщо вони не перетинаються (Рис. 13).

Теорема. Дві площини паралельні, якщо одна з них паралельна двом прямим, які лежать у другій площині і перетинаються (Рис. 14).

Теорема. Через точку поза даною площиною можна провести площину, паралельну даній, і до того ж тільки одну (Рис. 15).

Теорема. Якщо дві паралельні площини перетинаються третьою, то прямі їх перетину паралельні (Рис. 16).

Теорема. Відрізки паралельних прямих, які містяться між паралельними площинами, рівні (Рис. 17).

Для зворотнього зв'язку прошу пройти невеликий тест:

Перейдіть за посиланням  join.naurok.ua

Код доступу 171701

Бажаю успіху!!!



Урок № 9

Прямі та площини у просторі

З сьогоднішнього дня ми з вами починаємо повторювати все, що вивчили в цьому навчальному році. Тому кожен урок буде містити теоретичний матеріал та обов'зкове тестування.
Тож почнемо.

Означення. Стереометрія — це розділ геометрії, у якому вивчаються фігури у просторі.

Основними фігурами у просторі є точка, пряма і площина. Введення нового геометричного образу – площини, потребує розширення системи аксіом, тому ми вводимо групу аксіом С, яка виражає основні властивості площин у просторі.

С1. Яка б не була площина, існують точки, що належать цій площині, і точки, які не належать їй (Рис. 1).

С2. Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій (Рис. 2).

С3. Якщо дві різні прямі мають спільну точку, то через них можна провести площину, і до того ж тільки одну (Рис. 3).

Зауваження. У планіметрії ми мали одну площину, на якій розміщувались усі розглядувані нами фігури. У стереометрії нескінченно багато площин. У зв'язку з цим формулювання деяких аксіом потребують уточнення.

ІІ2. Пряма, яка належить площині, розбиває цю площину на дві півплощини.

IV2. Від півпрямої на площині, яка містить її, у задану півплощину можна відкласти кут заданої градусної міри, меншої 180°, і до того ж тільки один.

IV3. Який би не був трикутник, існує трикутник, що дорівнює йому, у даній площині із заданим розміщенням відносно даної пів прямої на цій площині.

V. На площині через точку, яка не лежить на даній прямій, можна провести не більше однієї прямої, паралельної даній.

Наслідки аксіом стереометрії

A, B, C - не лежать на одній прямій,
тоді !α, Aα, Bα, Cα
Рис. 6. Площина, проведена
через три точки

Якщо Aa, Ba, Aα, Bα
,тоді aαРис. 5. Пряма, яка проходить
через дві точки площини

Якщо Aa, тоді
!α , aα, Aα
Рис. 4. Площина, проведена
через пряму та точку

Теорема. Через пряму і точку, яка не лежить на ній, можна провести площину і до того ж тільки одну (Рис. 4).

Теорема. Якщо дві точки прямої належать площині, то вся пряма належить цій площині (Рис. 5).

3 теореми випливає, що площина і пряма, яка не лежить на ній, або не перетинаються, або перетинаються в одній точці.

Теорема. Через три точки, які не лежать на одній прямій, можна провести площину і до того ж тільки одну (Рис. 6).

Відкрийте посилання join.naurok.ua

Код доступу 985898

Бажаю успіху!!!

Урок № 8

Узагальнення матеріалу

Давайте ще раз перепровіремо ваші знання, але врахуємо все що ми вивчали на протягом року, для планування подальшої роботи.

Виконайте тест відкривши посилання join.naurok.ua

Код доступу 993075

Бажаю успіху!!!

Урок № 7




Урок № 6-7

Симетрія у просторі. Вектори у просторі.

Узагальнення матеріалу

Давайте з вами пригадаємо, все що ми вивчали в цій темі.

Для трьох векторів (ОА, ОС і ОО₁), які не лежать в одній площині й мають спільний початком (О), їхня сума зображується діагоналлю паралелепіпеда (ОВ₁), побудованого на цих векторах, причому початок вектора-суми збігається з початком цих векторів.

     Координати вектора-суми векторів дорівнюють сумі відповідних координат даних векторів.

Сума векторів у просторі

Різниця векторів у просторі

Множення вектора на число у просторі

Скалярним добутком двох векторів називається число, яке дорівнює сумі добутків відповідних координат цих векторів. Позначення таке саме, як і для добутку чисел, – .

Скалярний добуток двох векторів на площині

     Якщо є вектори , то .

     Теорема. Скалярний добуток двох векторів  дорівнює добутку довжин цих векторів на косинус кута між ними.

     Отже, .

   Якщо вектори перпендикулярні, то їхній скалярний добуток дорівнює нулю.

      І навпаки, якщо скалярний добуток відмінних від нуля векторів дорівнює нулю, то вектори перпендикулярні.

Поняття симетрії відносно прямої у просторі

Точки А і А₁ називаються симетрич­ними відносно прямої l, якщо пряма l проходить через середину відрізка АА₁ і перпендикулярна до нього (рис. 260).

Перетворення, яке відображає кожну точку фігури на точку, симетричну їй відносно даної прямої, називається симетрією відносно прямої (або осьовою симетрією).

Поняття симетрії відносно площини

Точки А і A₁ називаються симетричними відносно площини α, якщо ця площина перпендикулярна до відрізка АА₁ і ділить його пополам (рис. 262). Перетворення, при якому кожна точка даної фі­гури відображається на точку, симетричну їй відносно площини α, називається симетрією відносно площини α. Якщо перетворення симетрії відносно площини а переводить фігуру в себе, то фігура називається симетричною відносно площини α, а площина α нази­вається площиною симетрії.

Цей матеріал ми вже з вами вивчили. Спробуйте свої сили. розв'яжіть завдання поки що в своїх зошитах.

Узагальнення та систематизація  знань та вмінь учнів

Теоретичні  тестові завдання.

Вставте     пропущені     слова.

1. Вектор-це ………….
2. Щоб задати вектор, необхідні…..

точки.

3. Перша  точка - це……вектора,а друга …………вектора.

4. Якщо початок і кінець вектора  збігаються,то вектор називається….

5. Щоб знайти координати вектора, треба від координати ………вектора ….. координату ………вектора.

6. Якщо у двох векторів …….. координати рівні, то вектори називаються ………..

7. Довжиною вектора є ….. між його початком і кінцем.

8. За напрямом вектори бувають……

  І……, разом - ………

9. Якщо вектори колінеарні,то їх……

   координати……

10. Кутом між векторами є кут між їх…….

11. Сумою векторів є……….

12. Різницею векторів є………

13. Добутком числа на вектор є…….

14. Скалярним добутком векторів є ….……

15. Якщо скалярний добуток векторів дорівнює нулю, то вектори ………

16. Щоб знайти суму векторів треба ..….. їх …… координати.

17. Щоб знайти різницю векторів  треба ……. Їх …….. координати.

18. Щоб знайти добуток числа на вектор треба ……. координату вектора ……… на це число.

19. Щоб знайти скалярний добуток

     векторів, треба їх …….. координати…….. і отримані добутки ……  .

20. Якщо вектори задані відрізками, то їх суму або різницю можна знайти за правилами :

А) …………………………………..

Б)…………………………………….

В)…………………………………..

Відповіді на тестові завдання.

1. Напрямлений відрізок.

2. Дві.

3. Початок,кінець.

4. Нульовим.

5. Кінця, відняти, початку.

6. Відповідні, рівними.

7. Відстань.

8. Співнапрямлені, протилежно напрямлені, колінеарні.

9. Відповідні, пропорційні.

10. Напрямами.

11. Вектор.

12. Вектор.

13. Вектор.

14. Число.

15. Перпендикулярні.

16. Додати, відповідні.

17. Відняти, відповідні.

18. Кожну, помножити.

19. Відповідні, помножити, додати.

20. А) трикутника.

     Б) паралелограма.

     В) паралелепіпеда.

ПРАКТИЧНІ    ТЕСТОВІ ЗАВДАННЯ.

1. Знайдіть координати вектора

АВ,якщо  А(1;3;5), В(4;3;6).

2. Знайдіть модуль вектора

а(-3;0;4).

 

3. Знайдіть суму векторів

а(3;1;-2)  і  в(3;-2;5).

 

4. Знайдіть різницю векторів

а(3;-2; 0)  і  в( 1;-2; 4).

5. Знайдіть координати вектора

4а, якщо  а(1;-3; 4).

6. Знайдіть скалярний добуток

векторів  а(1;2;-3)   і

в(-8;2;4).

 7. При якому значенні   m   вектори  а(1;m;-3)  і   в(-2;10;6)  колінеарні?

     

     

8.При  якому  значенні  m   вектори  а(m; 4; -2)  і в(2;-4; -3) перпендикулярні?

  

   

9. Знайдіть довжину вектора 2а+3в, якщо а(2;0;-3),  в(5;-1;2).

   

  

10. Знайдіть кут між векторами  а(-2;0;2) і  в(0;0;4).

    

ВІДПОВІДІ  НА ПРАКТИЧНІ ТЕСТОВІ   ЗАВДАННЯ.

1. АВ(3;0;1)

2. 5

3. с (6;-1; 3)

4. с ( 2;0;-4)

5. 4а (4; -12; 16)

6. -16

7. m=-5

8. m=5

9. корінь  із  370

10. 45 градусів

Бажаю успіху!!! 


Урок № 5

Симетрія у просторі

Поняття симетрії відносно точки в просторі

Означення симетрії відносно точки, відоме з планіметрії, залишаєть­ся правильним і для стереометрії.

Точки А і А, називаються симетричними відносно точки О, якщо точка О — середина відрізка AA₁. Перетворення, при якому кожна точка даної фігури відображається на точку, симетричну їй відносно точки О, називається симетрією відносно точки О, або центральною симетрією. На рис. 257 відрізок АВ при симетрії відносно точки О переходить у відрізок A₁B₁. Якщо симетрія відносно деякої точки О відображає дану фігуру на ту саму фігуру, таку фігуру називають центрально-симетричною, а точку О — її центром симетрії. Наприклад, центрально-симетричною фігурою є прямокутний паралелепіпед, точка перетину його діагоналей — центр симетрії (рис. 258).

Розв'язування задач

1.     Дано точку А (і; 2; 3). Знайдіть координати точки А₁, симетричної точці А відносно початку координат. (Відповідь. А₁(-1;-2;-3).)

2.     Точки А (5; -3; 4) і В(-3; 1; - 2) симетричні відносно точки С. Знайдіть координати точки С. (Відповідь. С(1; -1; 1).)

3.     Точка А (1; 2; 3) симетрична точці В відносно точки С(3; 2; 1). Знайдіть координати точки В. (Відповідь. В (5; 2; -1).)

4.     Чи симетричні будь-які дві точки простору відносно деякої третьої точки?

5.     Скільки центрів симетрії має:

а) відрізок;   б) пряма;   в) коло;     г) площина;   д) куб?

6.     Дано куб. Побудуйте від руки фігуру, симетричну кубу відносно точки А(рис. 259).

Поняття симетрії відносно прямої у просторі

Точки А і А₁ називаються симетрич­ними відносно прямої l, якщо пряма l проходить через середину відрізка АА₁ і перпендикулярна до нього (рис. 260).

Перетворення, яке відображає кожну точку фігури на точку, симетричну їй відносно даної прямої, називається симетрією відносно прямої (або осьовою симетрією).

Розв'язування задач

1. Дано точку А (1; 2; 3). Знайдіть координати точки, симетричної їй відносно осі: а) х;     б) у;     в) z.

(Відповідь. А_x(1;-2;-3); А_y(-1; 2;-3); А_z(-1; -2; 3).)

2. Що таке вісь симетрії?

3. Скільки осей симетрії має:

а) відрізок;   б) пряма;    в) коло;    г) площина;   д) куб.

4. Дано куб. Побудуйте від руки фігуру, симетричну кубу відносно прямої АВ (рис. 261).

Поняття симетрії відносно площини

Точки А і A₁ називаються симетричними відносно площини α, якщо ця площина перпендикулярна до відрізка АА₁ і ділить його пополам (рис. 262). Перетворення, при якому кожна точка даної фі­гури відображається на точку, симетричну їй відносно площини α, називається симетрією відносно площини α. Якщо перетворення симетрії відносно площини а переводить фігуру в себе, то фігура називається симетричною відносно площини α, а площина α нази­вається площиною симетрії.

Розв'язування задач

Скільки площин симетрії має:

а) відрізок;   б) пряма;   в) коло;    г) площина; д) куб?

Дано куб. Побудуйте від руки фігуру, симетричну кубу відносно площини АВС (рис. 263).

Опрацювати конспект та виконати завдання в зошиті, представлені в конспекті.

Для зворотнього зв'язку заповни форму:

Бажаю успіху!!!

Урок № 4

 Дії з векторами у просторі. Колінеарність векторів у просторі. Скалярний добуток двох векторів. Ознака перпендикулярності векторів

   Шановні діти вивчаючи дану теми ви повинні  сформувати поняття операцій додавання, віднімання векторів, множення вектора на число у просторі; домогтися засвоєння властивостей цих операцій, правил трикутника, паралелограма, паралелепіпеда, знаходження суми векторів; сформувати вміння будувати вектор, що дорівнює сумі та різниці векторів, виконувати додавання, віднімання векторів, множення вектора на число у випадках, якщо вектори задані геометрично.

Сьогодні на уроці ми розберемо весь теоретичний матеріал та закріпимо його та прикладах. Тому Ваша задача скласти конспект, та заповнити форму в кінці уроку.

 Для трьох векторів (ОА, ОС і ОО₁), які не лежать в одній площині й мають спільний початком (О), їхня сума зображується діагоналлю паралелепіпеда (ОВ₁), побудованого на цих векторах, причому початок вектора-суми збігається з початком цих векторів.

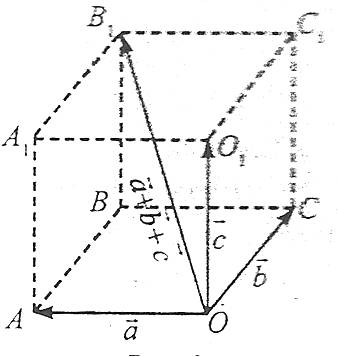
     Координати вектора-суми векторів дорівнюють сумі відповідних координат даних векторів.

Сума векторів у просторі

Різниця векторів у просторі

Множення вектора на число у просторі

Скалярним добутком двох векторів називається число, яке дорівнює сумі добутків відповідних координат цих векторів. Позначення таке саме, як і для добутку чисел, – .

Скалярний добуток двох векторів на площині

     Якщо є вектори , то .

     Теорема. Скалярний добуток двох векторів  дорівнює добутку довжин цих векторів на косинус кута між ними.

     Отже, .

   Якщо вектори перпендикулярні, то їхній скалярний добуток дорівнює нулю.

      І навпаки, якщо скалярний добуток відмінних від нуля векторів дорівнює нулю, то вектори перпендикулярні.

   

Заповнити форму за посиланням:
https://docs.google.com/forms/d/e/1FAIpQLSeesfkmjDXebaXidgEZLwgBekFToMzdiaFRgpeXs8KY7GO6EA/viewform?usp=sf_link


Урок № 3

 ВЕКТОРИ У ПРОСТОРІ

Шановні діти вивчаючи дану теми ви повинні: сформувати поняття вектора у просторі, рівних і колінеарних векторів, координат вектора; домогтися засвоєння формули для обчислення довжини (модуля) вектора, умови колінеарності векторів; сформувати вміння розв'язувати задачі, що передбачають використання цих понять.

Дайте відповіді на питання у своїх зошитах.

1. Сформулюйте означення вектора на площині.

2. Які вектори називають однаково напрямленими? протилежно напрямленими?

3. Що називають довжиною (модулем) вектора?

4. Який вектор називають нульовим?

5. Які вектори називають рівними? Чи можуть бути рівними вектори  і 

6. Як знайти координати вектора, якщо відомі координати його початку й кінця?

Це все ми з вами вивчали ще у 9 класі. Тож пригадати буде нескладно.

Хочу вам нагадати, але вибачте відео російською мовою

Давайте спробуємо знайти відповіді на наступні питання і порівняти з тим що ми вже з вами пригадали з 9 класу. В цьому вам допоможе наш підручник. 

§6 Координати та вектори у просторі
А саме п. 39  Вектори в просторі стр. 215

1. Означення вектора в просторі.
2. Означення нульового вектора.

3. Формули для знаходження координат вектора за координатами його початку й кінця.

4. Формула для обчислення довжини (модуля) вектора.

5. Означення рівних векторів. 
6. Основні властивості й ознаки рівних векторів.

7. Означення колінеарних векторів. 

8. Умова колінеарності векторів.

Спробуйте зробити висновок порівнявши вектори на площині та вектори у просторі.

Ну а тепер давайте попрацюємо, підручнику є пояснення тому звертаємося до підручника. 

Але у допомогу ще невеличке відео:

1) Знайдіть координати вектора  якщо M(10;-4;2), K(16;2;-5).

2) Знайдіть координати вектора  де точка O — початок координат, A(1;-3;2).

3) Знайдіть координати початку вектора  якщо 

4) При якому значенні n вектори  рівні?

5) При якому значенні n вектори  колінеарні?

6) Знайдіть довжину вектора , якщо A(2;-3;6), B(1;-1;4).

ABCDA₁B₁C₁D₁ — куб. Знайдіть координати векторів  якщо A(0;0;0), B(-3;0;0), D(0;3;0), A₁(0;0;3).

Опрацювавши даний матеріал наступний урок розпочнеться з опитування тож працюйте уважно, якщо є питання пишіть у блозі.

Урок № 1, 2

ПРЯМОКУТНІ КООРДИНАТИ В ПРОСТОРІ

Давайте пригадаємо

Ребро куба дорівнює 10: варіант 1 — рис. 252, варіант 2 — рис. 253. Запишіть координати точок: А, В, С, D, О, О1, А1, В1, С1, D1.

     

Твердження.

Квадрат, відстані між двома точками дорівнює сумі квад­ратів різниць їх відповідних координат.

Доведення

Нехай дано дві точки А(xA, уA, zA) і В(хB, yB, zB) (рис. 254). Доведе­мо, що АВ2 = (хB – xA)2 + (yB – уA)2 + (zB – zA)2. 

Розглянемо випадок, коли АВ не паралельна осі z. Через точки А і В проведемо прямі, паралельні осі z. Вони перетнуть площину ху в точках A1 і В1 відповідно. Ці точки мають ті самі координати х, у, що й точки А і В, а координата z їх однакова і дорівнює нулю. Проведемо через точку А площину, паралель­ну координатній площині ху. Побудована площина перетне пряму ВВ1 у деякій точці С, причому ВС = | zB – zA|. За теоремою Піфагора із ΔАВС маємо:

АВ2 = AC2 + ВС2. Оскільки АС2 = A1В12 = (хB – xA)2 + (yB – уA)2 ,

ВС = | zB – zA |, то АВ2 = (хB – xA)2 + (yB – уA)2 + (zB – zA)2.

Таким чином, відстань між точками А(xA, уA, zA) і В(хB, yB, zB) обчислюється за формулою .

Оформіть у зошиті конспект у вигляді таблиці

Для кращого розуміння пропоную переглянути відео за посиланням:

https://www.youtube.com/watch?v=-FWtWPTg0To

Опрацюйте у зошиті представлені задачі та порівняйте отримані відповіді із запропонованими

1. Знайдіть відстань АВ, якщо А(-1; 3; -1), В(-1; 0; - 5). (Відповідь. АВ = 5)

2. Знайдіть відстань від точки А(-1; 2; - 2) до початку координат.

(Відповідь. ОА = 3.)

3. Знайдіть периметр трикутника АВС, якщо А (7; 1; -5), В (4;-3;-4), C (1;3;-2). (Відповідь. 14 + )

4. Чи лежать точки А, В, С на одній прямій, якщо А(3;2;2), В(1;1;1), С(-1;0;0)? (Відповідь. Так.)

5. На якій відстані від координатних площин і координатних осей розташована точка А (- 2; 3; 4) ?

(Відповідь. ААx = 5; ААy = 2; ААz = ; ААxy = 4 ; ААxz = 3; ААyz = 2.)

6. Яка з точок — А (2; 1; 6) чи В (-2; 1; 6) — лежить ближче до почат­ку координат? (Відповідь. Точка А)

7. Дано точки К(0; 2; 1), Р(2; 0; 3) і T(-1; у; 0). Знайдіть таке зна­чення у, щоб виконувалась умова: КТ = РТ . (Відповідь. -3)

Виконані завдання сфотографуй та завантаж на google диск за посиланням: 

https://drive.google.com/drive/folders/1J2Z-osgNJSSljBXG6ReIFihNKU_bhodC?usp=sharing

Для зворотнього зв'язку виконайте завдання:
(якщо у відповіді буде дробове число запишіть його звичайним дробом через косу лінію "/")