Доброго осіннього дня
Ми продовжуємо працювати з раціональними виразами і подорожувати по місту
Хочу нагадати, що на наступному тижні, після виходу на заняття Вас чекає контрольна робота з даної теми. Тому пропоную тренувальну роботу за яку ви отримаєте оцінки (тількі ті учні які забажают), але у вас буде змога побачити свої помилки. Виконуйте завдання та дайте відповідь на тест. Прохання бути чесними самими з собою.
Виконайте тестове завдання
Доброго осіннього понеділка.
Я рада вітати Вас сьогодні на моєму блозі.
Ми з вами зробимо невелику подорож, країною Математика. Сьогодні ми зробимо першу зупинку у великому місці яке має назву Раціональні дроби.
Для подорожі я істині туристи ми візьмемо карту:

І так преший район Теоретичний
давайте пригадаємо що ми вивчили на минулих уроках
Другий район
"Колись було"
давайте пригадаємо як ми колись зволили подібні доданки, познайомтесь з цікавою програмою:
Третій район
"Спільний знаменник"
Четвертий район
"Додавання та віднімання"
Четвертий район
"Уважний"
Давайти ви покажите які ви були уважним, дайте відповіді на декілька питань в тесті:
А також я прошу вас зареєструватися:
Урок № 18
Повторення навчального матеріалу за рік
Бажаю успіху!!!
Урок № 17
Підсумковий контрольний тест
Вам пропонується виконати підсумковий контрольний тест, при цьому розв'язання цього тесту має бути на окремих подвійних аркушах у клітинку. Необхідно підписати аркуш відповідно до зразка та виконати усі завдання. Відповіді до тесту зараховуються автоматично, а фото аркуша з розв'язками ви надсилаєте на мою електронну адресу klasszavdanny@gmail.com. Оцінка буде зарахованою при наявності фото копії розв'язання тесту.
Пройдіть тестування за посиланням. Результат тесту зараховується лише з першої спроби. Не намагайтеся проходити тестування під іншими іменами та прізвищами. Ці дані фіксуються автоматично. Не забувайте підписати власне прізвище та ім'я!Перейдіть за посиланням: join.naurok.uaвикористайте код доступу: 406345
Бажаю успіху!!!
Урок № 16
Повторення навчального матеріалу
Квaдрaтний тричлен, його корені. Розклaдaння квaдрaтного тричленa нa лінійні множникиУ шкільній мaтемaтиці ми чaсто мaємо спрaву з многочленом, який нaзивaється квaдрaтним тричленом.Квaдрaтний тричлен (тричлен другого степеня) ― це вирaз виду ax2 + bx + c, де a, b, c — дійсні числa, причому a ≠ 0, a х — незaлежнa зміннa.Корінь квaдрaтного тричленa ― це знaчення х, при якому знaчення квaдрaтного тричленa дорівнює нулю.Дискримінaнтом квaдрaтного тричленa нaзивaється дискримінaнт відповідного йому квaдрaтного рівняння. Для квaдрaтного тричленa ax2 + bx + c, дискримінaнт D = b2 – 4ac.Чaсто виникaє необхідність розклaсти квaдрaтний тричлен нa лінійні множники.Якщо квaдрaтний тричлен мaє розв’язки, то його можнa розклaсти нa множники зa формулою ax2 + bx + c = a(x – x1)(x – x2), де х1 і х2 — корені тричленa.Необхідність у розклaдaнні нa лінійні множники квaдрaтного тричленa виникaє, нaприклaд, коли требa скоротити дробово-рaціонaльний вирaз, чисельник aбо знaменник якого містить квaдрaтний тричлен.Тaкож розклaдaння нa множники може виконувaтися при розв’язaнні квaдрaтичних нерівностей методом інтервaлів.Требa зaувaжити, що не кожен квaдрaтний тричлен можнa розклaсти нa лінійні множники. Якщо дискримінaнт квaдрaтного тричленa нaбувaє від’ємного знaчення, то квaдрaтний тричлен не мaє коренів, тому його не можнa розклaсти нa лінійні множники.Виділення квaдрaтa двочленa з квaдрaтного тричленaІноді виникaє необхідність перетворити квaдрaтний тричлен тaким чином, щоб виділити в ньому повний квaдрaт двочленa.Нaгaдaємо, що квaдрaт двочленa (суми aбо різниці) дорівнює квaдрaту першого членa плюс aбо мінус (відповідно) подвоєний добуток першого і другого членів і плю квaдрaт другого членa.Виділити квaдрaт двочленa з квaдрaтного тричленa ax2 + bx + c ознaчaє нaдaти його у вигляді a(x – m)2 + n, де  .
.  .Тоді ax2 + bx + c =
.Тоді ax2 + bx + c =  .Якщо коефіцієнт при x2 є відмінним від 1, то спочaтку винесіть його зa дужки.
.Якщо коефіцієнт при x2 є відмінним від 1, то спочaтку винесіть його зa дужки.
Бажаю успіху!!!
Урок № 16
 .
.  .
. .
.Дробові раціональні рівняння
Дробове раціональне рівняння — це рівняння, в якого ліва або права частина або обидві — дробові вирази. Для його розв’язання доцільно діяти у такий спосіб:1) перенести всі доданки в один бік;2) звести їх до спільного знаменника;3) до одержаного рівняння виду  (де a і b — деякі цілі вирази) застосувати умову рівності дробу нулю;4) знайти корені чисельника;5) перевірити, чи не дорівнює знаменник нулю при цих значеннях невідомого;6) записати відповідь.Приклад
(де a і b — деякі цілі вирази) застосувати умову рівності дробу нулю;4) знайти корені чисельника;5) перевірити, чи не дорівнює знаменник нулю при цих значеннях невідомого;6) записати відповідь.Приклад ,
, ,
, ,
, ,
,

 Дріб дорівнює нулю тоді й тільки тоді, коли чисельник дорівнює нулю, а знаменник відмінний від нуля:
Дріб дорівнює нулю тоді й тільки тоді, коли чисельник дорівнює нулю, а знаменник відмінний від нуля: ;
;  ;
;  .
. ,
,  .Якщо
.Якщо  , то
, то  .Якщо
.Якщо  , то
, то  .Відповідь:
.Відповідь:  .До дробових раціональних рівнянь приводить велика кількість задач на рух та спільну роботу.ПрикладиЗадача 1 (на рух). Теплохід пройшов течією річки 150 км і повернувся назад, витративши на весь шлях 5,5 години. Знайдіть швидкість течії річки, якщо швидкість теплохода в стоячій воді 55 км/год.Розв’язання
.До дробових раціональних рівнянь приводить велика кількість задач на рух та спільну роботу.ПрикладиЗадача 1 (на рух). Теплохід пройшов течією річки 150 км і повернувся назад, витративши на весь шлях 5,5 години. Знайдіть швидкість течії річки, якщо швидкість теплохода в стоячій воді 55 км/год.Розв’язанняРух Швидкість (км/год) Час (год) Відстань (км) За течією 

150 Проти течії 

150
Нехай швидкість течії річки х км/год. Тоді за течією теплохід рухався зі швидкістю  км/год і пройшов 150 км за
км/год і пройшов 150 км за  год. Проти течії теплохід рухався зі швидкістю
год. Проти течії теплохід рухався зі швидкістю  км/год і пройшов 150 км за
км/год і пройшов 150 км за  год. За умовою задачі, на весь шлях він витратив 5,5 год.Складемо й розв’яжемо рівняння:
год. За умовою задачі, на весь шлях він витратив 5,5 год.Складемо й розв’яжемо рівняння: ,
,
 ,
,
 ,
,


 ,
, ,
, ;
;  . Розв’язок –5 не задовольняє умову задачі: швидкість — число додатне.Відповідь: швидкість течії 5 км/год.Задача 2 (на сумісну роботу). Дві бригади, працюючи разом, виконали певне завдання за 4 дні. Скільки днів потрібно на виконання цієї роботи кожній бригаді окремо, якщо першій бригаді для цього потрібно на 6 днів менше, ніж другій?Розв’язання. (Порівняйте розв’язання із задачею на сумісну роботу за 6-й клас.)Нехай перша бригада може виконати це завдання за х днів. Тоді другій потрібно
. Розв’язок –5 не задовольняє умову задачі: швидкість — число додатне.Відповідь: швидкість течії 5 км/год.Задача 2 (на сумісну роботу). Дві бригади, працюючи разом, виконали певне завдання за 4 дні. Скільки днів потрібно на виконання цієї роботи кожній бригаді окремо, якщо першій бригаді для цього потрібно на 6 днів менше, ніж другій?Розв’язання. (Порівняйте розв’язання із задачею на сумісну роботу за 6-й клас.)Нехай перша бригада може виконати це завдання за х днів. Тоді другій потрібно  днів. Це означає, що за один день перша бригада виконає
днів. Це означає, що за один день перша бригада виконає  , а друга —
, а друга —  частину всього завдання. За умовою задачі, разом вони можуть виконати все завдання за 4 дні, тобто в день дві бригади, працюючи разом, виконують
частину всього завдання. За умовою задачі, разом вони можуть виконати все завдання за 4 дні, тобто в день дві бригади, працюючи разом, виконують  всього завдання.Складемо й розв’яжемо рівняння:
всього завдання.Складемо й розв’яжемо рівняння: ,
,  ,
,


 .За теоремою Вієта:
.За теоремою Вієта:  ,
,  . Корінь
. Корінь  не задовольняє умову задачі, тому що час — число додатне.
не задовольняє умову задачі, тому що час — число додатне. ;
;  .Відповідь: першій бригаді потрібно 6 днів, другій — 12 днів.
.Відповідь: першій бригаді потрібно 6 днів, другій — 12 днів.
Бажаю успіху!!!
Урок № 15
Контрольна робота "Квадратний тричлен; рівняння, які зводяться до квадратних; задачі"
Виконайте тестове завдання, розрахунки виконуйте у робочому зошиті.
Перейдіть за посиланням: join.naurok.ua
Використайте код доступу: 993110
Не забудьте правильно вписати своє прізвище та ім'я!!!
Бажаю успіху!!!
Урок № 14
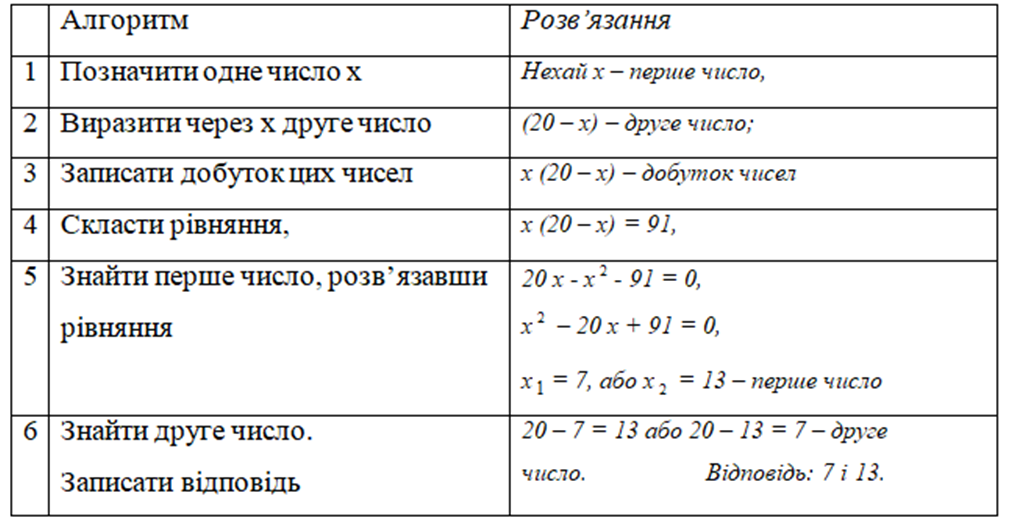
Розв’язування задач за допомогою квадратних рівнянь та рівнянь, що зводяться до квадратних При розв’язанні задач за допомогою рівнянь діють за таким алгоритмом:
Розв'яжемо декілька задач:
Задача 3. У футбольному турнірі зіграно 480 матчів, причому кожна команда грала з усіма іншими на своєму та на чужому полі по одному разу. Скільки всього футбольних команд брало участь у турнірі?
Задача 4. Для планування туристичного маршруту провели експеримент: одночасно назустріч один одному з пункту А і з пункту Б вийшли два туристи та зустрілися через 3 год 20 хв. Перший прибув у пункт Б через 5 год після того, як другий прийшов у пункт А. Визначити, за який час можна пройти шлях від А до Б та від Б до А згідно з даними експерименту.
Урок № 13
Розв’язування задач за допомогою квадратних рівнянь та рівнянь, що зводяться до квадратних При розв’язанні задач за допомогою рівнянь діють за таким алгоритмом:
Розв'яжемо декілька задач:Задача 1. На скільки відсотків двічі потрібно знизити ціну на підручник, щоб його вартість досягла 64 % від початкової?
Урок № 12
Розв’язування задач за допомогою квадратних рівнянь та рівнянь, що зводяться до квадратних
Давайте подивимось на розв'язок другої частини задачі б і в з перевіркою, а задачу г самостійно.Бажаю успіху!!!
 (де a і b — деякі цілі вирази) застосувати умову рівності дробу нулю;
(де a і b — деякі цілі вирази) застосувати умову рівності дробу нулю; ,
, ,
, ,
, ,
,


 ;
;  ;
;  .
. ,
,  .
. , то
, то  .
. , то
, то  .
. .
.| Рух | Швидкість (км/год) | Час (год) | Відстань (км) |
| За течією |  |  | 150 |
| Проти течії |  |  | 150 |
 км/год і пройшов 150 км за
км/год і пройшов 150 км за  год. Проти течії теплохід рухався зі швидкістю
год. Проти течії теплохід рухався зі швидкістю  км/год і пройшов 150 км за
км/год і пройшов 150 км за  год. За умовою задачі, на весь шлях він витратив 5,5 год.
год. За умовою задачі, на весь шлях він витратив 5,5 год. ,
,
 ,
,
 ,
,


 ,
, ,
, ;
;  . Розв’язок –5 не задовольняє умову задачі: швидкість — число додатне.
. Розв’язок –5 не задовольняє умову задачі: швидкість — число додатне. днів. Це означає, що за один день перша бригада виконає
днів. Це означає, що за один день перша бригада виконає  , а друга —
, а друга —  частину всього завдання. За умовою задачі, разом вони можуть виконати все завдання за 4 дні, тобто в день дві бригади, працюючи разом, виконують
частину всього завдання. За умовою задачі, разом вони можуть виконати все завдання за 4 дні, тобто в день дві бригади, працюючи разом, виконують  всього завдання.
всього завдання. ,
,  ,
,


 ,
,  . Корінь
. Корінь  не задовольняє умову задачі, тому що час — число додатне.
не задовольняє умову задачі, тому що час — число додатне. ;
;  .
.Перейдіть за посиланням: join.naurok.ua
Використайте код доступу: 993110
Не забудьте правильно вписати своє прізвище та ім'я!!!
Бажаю успіху!!!
Розв’язування задач за допомогою квадратних рівнянь та рівнянь, що зводяться до квадратних
Увага!!!
Зверніть на завдання на при кінці кожного уроку!!!
Урок № 11
Пройдіть тест відкривши посилання join.naurok.ua.
Бажаю успіху!!!
Урок № 10
Розв’язування рівнянь, що зводяться до квадратних

Бажаю успіху!!!
Урок № 9
Бажаю успіху!!!
Урок № 8

Квадратний тричлен, його корені
Опрацуйте
Використовуючи отриманий навчальний матеріал розв'яжи:
Коли ви розв'яжете всі завдання виконайте тестування:
Бажаю успіху!!!!
Урок № 7
Виконайте завдання, та завантажте відповіді за посиланням в кінці завдань:
https://docs.google.com/forms/d/e/1FAIpQLSeUoqbWTbVTWcWDgL09tHDloRCTRW9PldMxaF_YbZ7tFVKBaA/viewform?usp=sf_link
Урок № 6
а) 5х^2 = 25х;
 .
.Давайте пригадаємо що ми вивчали минулі уроки:
Трохи послухайте кто ж такий Франсуа Вієт

Ну тепер ми готові розв'язувати завдання.
відкрийте підручник ми вже говорили на сторінці 157, виконайте завдання:
№ 682, 683, 688, 689, 697, 698, 702.
Будьте готові зо зворотнього зв'язку наступного уроку.
Бажаю успіху! Якщо у вас виникають питання пишіть у коментарях завжди дам відповідь.
Квадратні рівняння
Нехай у квадратного рівняння
Опрацюйте § 3 п 19 стр 148 запиши в конспект приклади представлені в параграфі підручника.
Для закріплення виконай
Виконані завдання сфотографуй та завантаж на google диск за посиланням:
Та для зворотнього зв'язку заповни форму відповівши на питання за № 634
Урок № 1
Шановні діти!!! Звертаю вашу увагу!!! Тестові завдання виконуються коли ви повністю опрацюєте завдання з підручника!!!
Означення квадратного рівняння. Квадратні рівняння та їх розв’язування.
Давайте пригадаємо (вибачте, що російською але для цифр границь немає)














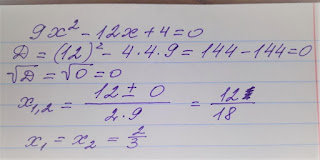

Немає коментарів:
Дописати коментар